Содержание

1. Интерфейс
2. Теория
   1. Валидность
   2. Надежность
      1. Надежность как устойчивость
      2. Надежность как внутренняя согласованность
   3. Дискриминативность
3. Интерпретация результата
4. Рекомендации для тестолога

Валидность

1. Валидность — пригодность тестовых результатов для той цели, ради чего проводилось тестирование.
2. Валидность — это характеристика способности теста служить поставленной цели измерения.
3. Валидность — определяет, насколько тест отражает то, что он должен оценивать.

Для оценки валидности теста обычно используют корреляцию между показателями теста и некоторым внешним критерием. При такой оценке очень важно выбрать значимый внешний критерий. Для педагогических тестов в качестве критерия обычно берутся оценки экспертов, выставленные ими при традиционной проверке знаний студентов без использования тестов. Процесс валидизации осложняется необходимостью установления меры согласованности оценок экспертов, которых обычно бывает не менее трех человек.

$$ V = \frac{\frac{1}{n}\left ( \sum\limits_{i=1}^n Y_{i} \cdot y_{i} \right )- \overline{Y}\cdot \overline{y}}{S_{Y}\cdot S_{y}} \cdot \frac{n}{n-1}. $$

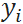	количество правильных ответов	известно
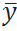	средняя арифметическая тестовых баллов тестируемых	$$ = \frac{1}{n}\sum\limits_{i=1}^n y_{i} $$
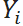	экспертная оценка	известно
	среднее арифметическое экспертных оценок	$$ = \frac{1}{n}\sum\limits_{i=1}^n Y_{i} $$
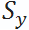	стандартное отклонение количества правильных оценок	$$ =\sqrt{\frac{1}{n-1}\sum\limits_{i=1}^n (y_{i} - \overline{y})^{2}} $$
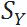	стандартное отклонение экспертных оценок	$$ =\sqrt{\frac{1}{n-1}\sum\limits_{i=1}^n (Y_{i} - \overline{Y})^{2}} $$

Надежность

Надежностью называется характеристика теста, отражающая точность тестовых измерений, а также устойчивость тестовых результатов к действию случайных факторов. Во-первых, тест считается надежным, если он обеспечивает высокую точность измерений. И во-вторых, тест считается надежным, если он дает при повторном выполнении близкие результаты при условии, что подготовка ученика не изменилась за время до повторного выполнения теста. Таким образом будем считать, что надежность теста показывает, на сколько точно тест измеряет знания студентов или другие явления. Надежность характеризует точность теста как измерительного инструмента, устойчивость его к действию помех.
Различают два вида надежности:
1. надежность как устойчивость
2. надежность как внутреннюю согласованность.

Однако большинство авторов предпочитают рассматривать только надежность как внутреннюю согласованность, так как этот вид измерений требует проведение тестирование только один раз. В случае надежность как внутренняя согласованность проводить тестирование приходится два раза.

Надежность как устойчивость

Надежность как устойчивость измеряется с помощью повторного проведения теста на той же выборке испытуемых, обычно через две недели после первого тестирования. Для нахождения данной характеристики предлагается использовать формулу Пирсона.

$$ V = \frac{n \sum\limits_{i=1}^n X_{i} Y_{i} - \sum\limits_{i=1}^n X_{i} \cdot \sum\limits_{i=1}^n Y_{i}} {\sqrt{n \sum\limits_{i=1}^n X_{i}^2 - \left ( \sum\limits_{i=1}^n X_{i} \right )^2}{\sqrt{n \sum\limits_{i=1}^n Y_{i}^2 - \left ( \sum\limits_{i=1}^n Y_{i} \right )^2}}} $$

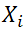	тестовый балл i-го испытуемого при первом измерении
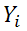	тестовый балл i-го испытуемого при повторном измерении

Надежность как внутренняя согласованность

Для проверки внутренней согласованности предлагается метод расщепления (автономных частей). При применении метода расщепления тестовую матрицу разбивают на две половины, состоящие из заданий с четными и нечетными номерами. Используя формулу Рюлона, найдем нужный нам коэффициент.

$$ r = 1 -\frac{S_{d}^{2}}{S_{Z}^{2}} $$

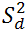	дисперсия разностей между результатами каждого испытуемого по обеим половинам теста	$$ = \frac{1}{n-1}\sum\limits_{i=1}^n \left ( (X_{i} - Y_{i}) - \frac{1}{n}\sum\limits_{i=1}^n(X_{i} - Y_{i})\right )^2 $$
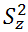	дисперсия суммарных баллов результата	$$ = \frac{1}{n-1}\left (\frac{1}{n}\sum\limits_{i=1}^n Z_{i} - Z_{i}\right )^2 $$
	количество правильных ответов
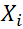	количество правильных ответов c четным номером
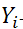	количество правильных ответов c нечетным номером
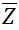	среднее арифметическое количества правильных ответов	$$ = \frac{1}{n}\sum\limits_{i=1}^n Z_{i} $$
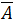	обозначение	$$ = \frac{1}{n}\sum\limits_{i=1}^n (X_{i} - Y_{i}) $$

Дискриминативность

Дискриминативность задач определяется как способность отделять испытуемых с высоким общим баллом по тесту от тех, кто получил низкий балл, или испытуемых с высокой продуктивностью учебной деятельности от испытуемых с низкой продуктивностью.

Другими словами, дискриминативность — способность заданий теста дифференцировать студентов относительно "максимального" или "минимального" результата теста. Определение дискриминативности тестового задания необходимо для того, чтобы поставить заслон некачественным заданиям.

Для вычисления дискриминативности будет применяться метод крайних групп: при расчете дискриминативности тестового задания учитываются результаты наиболее и наименее успешных студентов — это самый простой и наглядный метод вычисления дискриминативности.

Доля членов крайних групп может изменяться в широких пределах в зависимости от величины выборки. Чем больше выборка, тем меньшей долей испытуемых можно ограничиться при выделении групп с высоким и низким результатами. Нижняя граница "отсечения групп" составляет 10% от общего числа испытуемых в выборке, верхняя — 33%. В данном случае будет использоваться 27% группа, так как при таком процентном соотношении достигается максимальная точность определения дискриминативности. Индекс дискриминации вычисляется как разность между долей лиц, правильно решивших задачу, из "высокопродуктивной" и "низкопродуктивной" групп.

$$ D = \frac{N_{n_{max}}}{N_{max}} - \frac{N_{n_{min}}}{N_{min}} $$

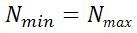	общее количество испытуемых крайних группах	27% от всего количества
	количество студентов в группе худших, верно выполнивших задание
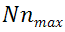	количество студентов в группе лучших, верно выполнивших задание
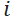	номер тестового задания
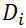	коэффициент дискриминативоности тестового задания	по основной формуле

Интерпретация

Валидность

Надежность

Дискриминативность

Рекомендации для тестолога

1. Если тест рассматривать как средство контроля качества знаний обучаемых, то, прежде всего, необходимо совершенствовать форму тестовых заданий с целью повышения качества педагогического измерения, включая в тест не только задания с выбором одного правильного ответа, но и выбором нескольких правильных ответов. Безусловно, задания с выбором одного правильного ответа удобно использовать при автоматизированном контроле знаний (так составлены педагогические тесты для централизованного тестирования по математике). Однако с помощью таких заданий далеко не всегда можно качественно проверить знания испытуемых в силу того, что слишком велика вероятность угадывания правильных ответов. Такого недостатка лишены задания с выбором нескольких правильных ответов и задания открытой формы, а интенсивное развитие информационных технологий позволяет включить их в педагогический тест и при автоматизированном контроле знаний.
2. Если рассматривать тест как средство обучения, предназначенное для формирования системы знаний обучаемых, то в педагогической практике целесообразно использовать комплексы тематических тестов по изучаемой дисциплине. Эти комплексы должны состоять не только из тестов для проверки практических умений и навыков обучаемых, но и из тестов для проверки их теоретических знаний, которые являются ядром формируемой педагогом системы знаний обучаемых.
3. Если Вы хотите составить тестовые задания, обладающие удовлетворительной дискриминативностью, то необходимо избегать следующего:
   1. излишней сложности и запутанности формулировок;
   2. неоднозначности условий;
   3. очевидности решения;
   4. зависимости результата от памяти или от других индивидуальных особенностей испытуемого, а не от уровня развития тех умений и навыков, для оценки которых разрабатывается тест;
   5. абсурдности, нереальности вариантов ответов;
   6. появления двух и более правильных ответов, не оговоренных в условии.
4. Если Вы хотите повысить валидность теста, то:
   1. составляйте тестовые задания оптимальной трудности для обеспечения нормального закона распределения баллов по тесту;
   2. проводите экспертизу качества содержания теста;
   3. правильно рассчитывайте оптимальное время выполнения теста;
   4. включайте в тест задания с высокой дискриминативностью.
5. Если Вы хотите повысить надежность теста, то по возможности устраните влияние на Ваш тест следующих факторов:
   1. субъективизма при оценке результатов выполнения заданий теста, используя для этого задания закрытого типа;
   2. угадывания, которое существенно снижает надежность теста, особенно в тех случаях, когда тестируется группа слабых учеников, которые обычно прибегают к догадке при выполнении наиболее трудных заданий теста;
   3. некорректно сформулированных заданий, поскольку такие задания пропускают сильные ученики, что в целом негативно отражается на надежности теста;
   4. неоправданного выбора весовых коэффициентов;
   5. неоправданной длины теста, так как его надежность растет по мере увеличения длины, и для удовлетворительной, но не хорошей надежности, обычно достаточно 30 тестовых заданий;
   6. отсутствия стандартной инструкции к тесту, так как любые неоднозначности, двусмысленности и отступления от требований стандартизации в инструкции ведут к снижению надежности теста;
   7. источников ненадежности, связанных с испытуемыми, а не с заданиями теста (плохого самочувствия испытуемого, его усталости и скуки, шума в аудитории и т.п.).
6. Иногда при нахождении коэффициента надежности происходит деление на нуль. Это может произойти, если все испытуемые имеют одинаковое количество правильных и неправильных ответов. Такое редко бывает на практике, скорее всего, произошла утечка ответов. В данном случае следует провести тест повторно.
7. При нахождении надежности как устойчивости, так же возможен случай, который дает в ответе неопределенность, т.е. происходит деление нуля на нуль. Такое может произойти, когда испытуемый дал одинаковое количество правильных и неправильных ответов на первом и повторном тестировании. Это означает, что тест составлен очень удачно или же наоборот, очень неудачно. Советуем вам проверить другие тестовые характеристиками и, исходя из них, сделать заключение.
8. При расчете валидности также возможен случай, когда происходит деление на нуль. Это может произойти в том случае, если все испытуемые имеют одинаковое количество правильных и неправильных ответов или, если все экспертные оценки одинаковы. Такой случай редко может произойти на практике, скорее всего, произошла утечка ответов, и данный результат искажен.